부모 노드와 자식 노드로 이루어진 계층 구조
무방향 그래프의 일종, 사이클이 없는 자료구조이다.
노드간 경로는 반드시 존재하며, 반드시 하나이다.

루트노드 - 부모노드
내부노드 - 부모노드와 리프노드 사이의 노드
리프노드 - 자식이 없는 마지막 계층의 노드
Vertex - 1 = Edge
Vertex 갯수는 6, Edge의 갯수는 5이다.
Vetex 갯수 - 1 = Edge 갯수이다.
트리 내에 트리의 구조를 띄는 구조를 서브트리라고 한다.
루트노드부터 리프노드까지의 가장 긴 거리는 높이이다.
서브트리에서 루트노드부터 리프노드까지의 최단거리는 깊이, 레벨이다.
이진 트리
자식 노드의 수가 2개 이하인 트리.

균형 이진트리가 알고리즘에서 가장 중요하다.
균형이진트리는 모든 노드에서 봤을 때, 왼쪽 하위 트리와 오른쪽 하위 트리의 높이차가 1 이하인 이진트리이다.
균형 이진트리에는 레드블랙트리가 있는데 map과 set은 레드블랙트리의 구조로, O(logn)의 시간복잡도를 가진다.
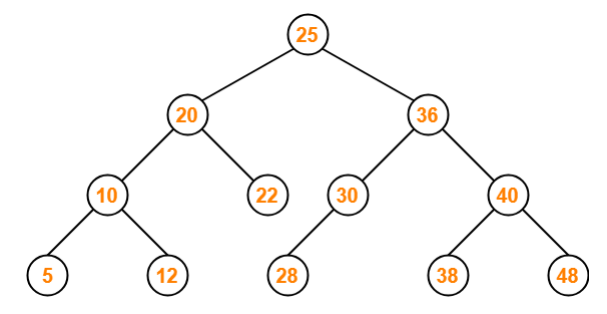
이진탐색트리
이진트리의 일종이다.
왼쪽 하위노드에는 노드보다 작은 값, 오른쪽 하위노드에는 노드의 값보다 큰 값이 들어간다.
트리 순회
트리 구조에서 각 노드들을 정확히 한 번만 방문하는 과정.
서브트리를 탐색해야 하기 때문에 재귀함수를 사용한다.
1. 후위 순회
자식노드부터 방문한다.
postorder( node )
if (node.visited == false)
postorder( node->left )
postorder( node->right )
node.visited = true
2. 전위 순회
자신의 노드부터 방문하고 다음 노드를 방문한다. = DFS
preorder( node )
if (node.visited == false)
node.visited = true
preorder( node->left )
preorder( node->right )
3. 중위 순회
왼쪽, 자신, 오른쪽 노드 순으로 방문한다.
inorder( node )
if (node.visited == false)
inorder( node->left )
node.visited = true
inorder( node->right )
#include <bits/stdc++.h>
using namespace std;
vector<int> adj[1004];
int visited[1004];
void postOrder(int here)
{
if (visited[here] == 0)
{
if (adj[here].size() == 1)
postOrder(adj[here][0]);
if (adj[here].size() == 2)
{
postOrder(adj[here][0]);
postOrder(adj[here][1]);
}
visited[here] = 1;
cout << here << ' ';
}
}
void preOrder(int here)
{
if (visited[here] == 0)
{
visited[here] = 1;
cout << here << ' ';
if (adj[here].size() == 1)
preOrder(adj[here][0]);
if (adj[here].size() == 2)
{
preOrder(adj[here][0]);
preOrder(adj[here][1]);
}
}
}
void inOrder(int here)
{
if (visited[here] == 0)
{
if (adj[here].size() == 1)
{
inOrder(adj[here][0]);
visited[here] = 1;
cout << here << ' ';
}
else if (adj[here].size() == 2)
{
inOrder(adj[here][0]);
visited[here] = 1;
cout << here << ' ';
inOrder(adj[here][1]);
}
else
{
visited[here] = 1;
cout << here << ' ';
}
}
}
int main()
{
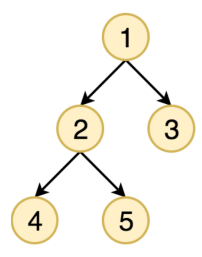
adj[1].push_back(2);
adj[1].push_back(3);
adj[2].push_back(4);
adj[2].push_back(5);
int root = 1;
cout << "\n 트리순회 : postOrder \n";
postOrder(root);
memset(visited, 0, sizeof(visited));
cout << "\n 트리순회 : preOrder \n";
preOrder(root);
memset(visited, 0, sizeof(visited));
cout << "\n 트리순회 : inOrder \n";
inOrder(root);
return 0;
}
'Study > 알고리즘 이론' 카테고리의 다른 글
| BFS, 너비 우선 탐색 (0) | 2024.09.16 |
|---|---|
| DFS, 깊이 우선 탐색 (0) | 2024.09.16 |
| 그래프 (1) | 2024.09.15 |
| 백준 C++ 시간초과 (0) | 2024.09.14 |
| 누적합 Prefix sum (0) | 2024.09.12 |